This code is used to convert binary number into octal, decimal and hexadecimal and vice versa.
clear
i=1
while [ $i -eq 1 ]
do
clear
echo "Enter the input base type"
echo "1.binary"
echo "2.Octal"
echo "3.Decimal"
echo "4.Hexadecimal"
echo "Enter your choice"
read ch
echo "Enter Number to be converted.: "
read inp
if [ $ch -eq 1 ]
then
echo "Enter the input base type"
echo "1.Octal"
echo "2.Decimal"
echo "3.Hexadecimal"
echo "Enter your choice"
read ch2
if [ $ch2 -eq 1 ]
then
echo "Base after converting is "
echo "obase=8;ibase=2;$inp" | bc
fi
if [ $ch2 -eq 2 ]
then
echo "Base after converting is "
echo "obase=10;ibase=2;$inp" | bc
fi
if [ $ch2 -eq 3 ]
then
echo "Base after converting is "
echo "obase=16;ibase=2;$inp" | bc
fi
fi
if [ $ch -eq 2 ]
then
echo "Enter the input base type"
echo "1.Binary"
echo "2.Decimal"
echo "3.Hexadecimal"
echo "Enter your choice"
read ch2
if [ $ch2 -eq 1 ]
then
echo "Base after converting is "
echo "obase=2;ibase=8;$inp" | bc
fi
if [ $ch2 -eq 2 ]
then
echo "Base after converting is "
echo "obase=10;ibase=8;$inp" | bc
fi
if [ $ch2 -eq 3 ]
then
echo "Base after converting is "
echo "obase=16;ibase=8;$inp" | bc
fi
fi
if [ $ch -eq 3 ]
then
echo "Enter the input base type"
echo "1.Binary"
echo "2.Octal"
echo "3.Hexadecimal"
echo "Enter your choice"
read ch2
if [ $ch2 -eq 1 ]
then
echo "Base after converting is "
echo "obase=2;ibase=10;$inp" | bc
fi
if [ $ch2 -eq 2 ]
then
echo "Base after converting is "
echo "obase=8;ibase=10;$inp" | bc
fi
if [ $ch2 -eq 3 ]
then
echo "Base after converting is "
echo "obase=16;ibase=10;$inp" | bc
fi
fi
if [ $ch -eq 4 ]
then
echo "Enter the input base type"
echo "1.Binary"
echo "2.Octal"
echo "3.Decimal"
echo "Enter your choice"
read ch2
if [ $ch2 -eq 1 ]
then
echo "Base after converting is "
echo "obase=2;ibase=16;$inp" | bc
fi
if [ $ch2 -eq 2 ]
then
echo "Base after converting is "
echo "obase=8;ibase=16;$inp" | bc
fi
if [ $ch2 -eq 3 ]
then
echo "Base after converting is "
echo "obase=10;ibase=16;$inp" | bc
fi
fi
echo "Enter 1 to continue else 0 ?"
read i
if [ $i -eq 0 ]
then
echo "Exit."
exit
fi
done
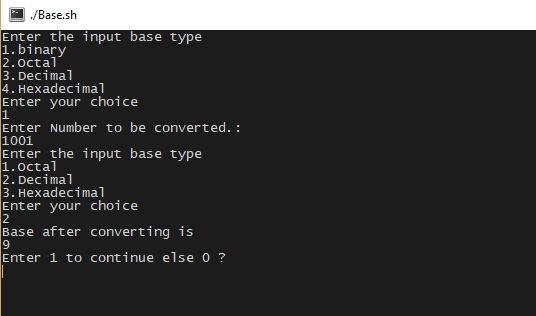
OUTPUT:
BINARY NUMBER SYSTEM
In mathematics, positional numeral system employing 2 as the base and so requiring only two different symbols for its digits, 0 and 1, instead of the usual 10 different symbols needed in the decimal system. The numbers from 0 to 10 are thus in binary 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, and 1010. The importance of the binary system to information theory and computertechnology derives mainly from the compact and reliable manner in which 0s and 1s can be represented in electromechanical devices with two states—such as “on-off,” “open-closed,” or “go–no go.”
The binary number system, also called the base-2 number system, is a method of representing numbers that counts by using combinations of only two numerals: zero (0) and one (1). Computers use the binary number system to manipulate and store all of their data including numbers, words, videos, graphics, and music.
The term bit, the smallest unit of digital technology, stands for “BInary digiT.” A byte is a group of eight bits. A kilobyte is 1,024 bytes or 8,192 bits.In-System Programmers – DatamanJTAG Compatible ISP Interface, Free Software, 3 Year Warranty, Buy Today!dataman.com | Sponsored▼
Using binary numbers, 1 + 1 = 10 because “2” does not exist in this system. A different number system, the commonly used decimal or base-10 number system, counts by using 10 digits (0,1,2,3,4,5,6,7,8,9) so 1 + 1 = 2 and 7 + 7 = 14. Another number system used by computer programmers is the hexadecimal system, base-16 , which uses 16 symbols (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F), so 1 + 1 = 2 and 7 + 7 = E. Base-10 and base-16 number systems are more compact than the binary system. Programmers use the hexadecimal number system as a convenient, more compact way to represent binary numbers because it is very easy to convert from binary to hexadecimal and vice versa. It is more difficult to convert from binary to decimal and from decimal to binary.Report Advertisement
The advantage of the binary system is its simplicity. A computing device can be created out of anything that has a series of switches, each of which can alternate between an “on” position and an “off” position. These switches can be electronic, biological, or mechanical, as long as they can be moved on command from one position to the other. Most computers have electronic switches.Computers – Shop Now at Best Buy®Price Match Guarantee. Free Shipping $35 & Up Or Ready In One Hour!deals.bestbuy.com/DigitalInsert | Sponsored▼
When a switch is “on” it represents the value of one, and when the switch is “off” it represents the value of zero. Digital devices perform mathematical operations by turning binary switches on and off. The faster the computer can turn the switches on and off, the faster it can perform its calculations.
| Binary | Decimal | Hexadecimal |
| Number | Number | Number |
| System | System | System |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 10 | 2 | 2 |
| 11 | 3 | 3 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
| 1000 | 8 | 8 |
| 1001 | 9 | 9 |
| 1010 | 10 | A |
| 1011 | 11 | B |
| 1100 | 12 | C |
| 1101 | 13 | D |
| 1110 | 14 | E |
| 1111 | 15 | F |
| 10000 | 16 | 10 |
Positional Notation
Each numeral in a binary number takes a value that depends on its position in the number. This is called positional notation. It is a concept that also applies to decimal numbers.
For example, the decimal number 123 represents the decimal value 100 + 20 + 3. The number one represents hundreds, the number two represents tens, and the number three represents units. A mathematical formula for generating the number 123 can be created by multiplying the number in the hundreds column (1) by 100, or 102; multiplying the number in the tens column (2) by 10, or 101; multiplying the number in the units column (3) by 1, or 100; and then adding the products together. The formula is: 1 × 102 + 2 × 101 + 3 × 100 = 123.
This shows that each value is multiplied by the base (10) raised to increasing powers. The value of the power starts at zero and is incremented by one at each new position in the formula.
This concept of positional notation also applies to binary numbers with the difference being that the base is 2. For example, to find the decimal value of the binary number 1101, the formula is 1 × 23 + 1 ×22 + 0 × 21 + 1 × 20 = 13.
Binary Operations
Binary numbers can be manipulated with the same familiar operations used to calculate decimal numbers, but using only zeros and ones. To add two numbers, there are only four rules to remember:
Therefore, to solve the following addition problem, start in the rightmost column and add 1 + 1 = 10; write down the 0 and carry the 1. Working with each column to the left, continue adding until the problem is solved.
To convert a binary number to a decimal number, each digit is multiplied by a power of two. The products are then added together. For example, to translate the binary number 11010 to decimal, the formula would be as follows:
To convert a binary number to a hexadecimal number, separate the binary number into groups of four starting from the right and then translate each group into its hexadecimal equivalent. Zeros may be added to the left of the binary number to complete a group of four. For example, to translate the number 11010 to hexadecimal, the formula would be as follows:
Digital Data
Bits are a fundamental element of digital computing. The term “digitize” means to turn an analog signal—a range of voltages—into a digital signal, or a series of numbers representing voltages. A piece of music can be digitized by taking very frequent samples of it, called sampling, and translating it into discrete numbers, which are then translated into zeros and ones. If the samples are taken very frequently, the music sounds like a continuous tone when it is played back.
A black and white photograph can be digitized by laying a fine grid over the image and calculating the amount of gray at each intersection of the grid, called a pixel . For example, using an 8-bit code, the part of the image that is purely white can be digitized as 11111111. Likewise, the part that is purely black can be digitized as 00000000. Each of the 254 numbers that fall between those two extremes (numbers from 00000001 to 11111110) represents a shade of gray. When it is time to reconstruct the photograph using its collection of binary digits, the computer decodes the image, assigns the correct shade of gray to each pixel, and the picture appears. To improve resolution, a finer grid can be used so the image can be expanded to larger sizes without losing detail.
A color photograph is digitized in a similar fashion but requires many more bits to store the color of the pixel. For example, an 8-bit system uses eight bits to define which of 256 colors is represented by each pixel (28 equals 256). Likewise, a 16-bit system uses sixteen bits to define each of 65,536 colors (216equals 65,536). Therefore, color images require much more storage space than those in black and white.
Octal Number System
In early days octal number system was mostly used in minicomputers. The word “OCT” means eight. The octal number system says that it is a number system of base 8 which means that we require 8 different symbols in order to represent any number in octal system. The symbols are 0, 1, 2, 3, 4, 5, 6, and 7. The smallest two digit number in this system is (10)8 which is equivalent to decimal 8.
For example in this number system, the number is written as (352)8. The base should be written as 8 otherwise the number is assumed to be in decimal number system by default. So this thing needs to be taken care of in writing the number. A little error may result in the change in number system base. The main advantage of using octal number system is that it can be converted directly to binary in a very easy manner. As we know, the computer understands only the binary number system, so the conversion from binary to octal or from octal to binary is quite easier so this number system is used.


As its base is 8 = 23, every symbol of this system can be represented by its three bit binary equivalent.
As every digit of a number in octal system is represented separately by its three bit binary equivalent the octal system requires one-third of the length as compared to binary numbers. It is basically a positional weighted number system. The digit positions in octal number system has weight as
Advantages of Octal Number Systems
- It is of one third length of the binary.
- Easy conversion process from binary to octal and vice-versa.
- Easier to handle input and output in the octal form.
Disadvantages of Octal Number Systems
Computer does not understand octal number system so there must be a requirement of additional circuitry known as octal to binary converters before it is applied to a digital system or a computer.
Decimal Number System
Decimal is a term that describes the base-10 number system, probably the most commonly used number system. The decimal number system consists of ten single- digit numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The number after 9 is 10. The number after 19 is 20 and so forth. Additional powers of 10 require the addition of another positional digit.
In computing, the binary , octal , or hexadecimalnumber system may be used instead of the decimal system. All these schemes have a number of digits that is a power of 2. This is an advantage in systems that use high and low digital states.
| Decimal | Binary | Octal | Hexadecimal |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
| 17 | 10001 | 21 | 11 |
| etc | etc | etc | etc |
Hexadecimal Numbers SYSTEM
Hexadecimal Numbers group binary numbers into sets of four allowing for the conversion of 16 different binary digits
The one main disadvantage of binary numbers is that the binary string equivalent of a large decimal base-10 number can be quite long.
When working with large digital systems, such as computers, it is common to find binary numbers consisting of 8, 16 and even 32 digits which makes it difficult to both read or write without producing errors especially when working with lots of 16 or 32-bit binary numbers.
One common way of overcoming this problem is to arrange the binary numbers into groups or sets of four bits (4-bits). These groups of 4-bits uses another type of numbering system also commonly used in computer and digital systems called Hexadecimal Numbers.
Hexadecimal Number String
The “Hexadecimal” or simply “Hex” numbering system uses the Base of 16 system and are a popular choice for representing long binary values because their format is quite compact and much easier to understand compared to the long binary strings of 1’s and 0’s.
Being a Base-16 system, the hexadecimal numbering system therefore uses 16 (sixteen) different digits with a combination of numbers from 0 through to 15. In other words, there are 16 possible digit symbols.
However, there is a potential problem with using this method of digit notation caused by the fact that the decimal numerals of 10, 11, 12, 13, 14 and 15 are normally written using two adjacent symbols. For example, if we write 10 in hexadecimal, do we mean the decimal number ten, or the binary number of two (1 + 0). To get around this tricky problem hexadecimal numbers that identify the values of ten, eleven, . . . , fifteen are replaced with capital letters of A, B, C, D, E and F respectively.
Then in the Hexadecimal Numbering System we use the numbers from 0 to 9 and the capital letters A to F to represent its Binary or Decimal number equivalent, starting with the least significant digit at the right hand side.
As we have just said, binary strings can be quite long and difficult to read, but we can make life easier by splitting these large binary numbers up into even groups to make them much easier to write down and understand. For example, the following group of binary digits 1101 0101 1100 11112 are much easier to read and understand than11010101110011112 when they are all bunched up together.
In the everyday use of the decimal numbering system we use groups of three digits or 000’s from the right hand side to make a very large number such as a million or trillion, easier for us to understand and the same is also true in digital systems.
Hexadecimal Numbers is a more complex system than using just binary or decimal and is mainly used when dealing with computers and memory address locations. By dividing a binary number up into groups of 4 bits, each group or set of 4 digits can now have a possible value of between “0000” (0) and “1111” ( 8+4+2+1 = 15 ) giving a total of 16different number combinations from 0 to 15. Don’t forget that “0” is also a valid digit.
We remember from our first tutorial about Binary Numbers that a 4-bit group of digits is called a “nibble” and as 4-bits are also required to produce a hexadecimal number, a hex digit can also be thought of as a nibble, or half-a-byte. Then two hexadecimal numbers are required to produce one full byte ranging from 00 to FF.
Also, since 16 in the decimal system is the fourth power of 2 ( or 24 ), there is a direct relationship between the numbers 2 and 16 so one hex digit has a value equal to four binary digits so now q is equal to “16”.
Because of this relationship, four digits in a binary number can be represented with a single hexadecimal digit. This makes conversion between binary and hexadecimal numbers very easy, and hexadecimal can be used to write large binary numbers with much fewer digits.
The numbers 0 to 9 are still used as in the original decimal system, but the numbers from 10 to 15 are now represented by capital letters of the alphabet from A to F inclusive and the relationship between decimal, binary and hexadecimal is given below.
Hexadecimal Numbers
| Decimal Number | 4-bit Binary Number | Hexadecimal Number |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
| 16 | 0001 0000 | 10 (1+0) |
| 17 | 0001 0001 | 11 (1+1) |
| Continuing upwards in groups of four |
Using the original binary number from above 1101 0101 1100 11112 this can now be converted into an equivalent hexadecimal number of D5CF which is much easier to read and understand than a long row of 1’s and 0’s that we had before.
So by using hexadecimal notation, digital numbers can be written using fewer digits and with a much less likelihood of an error occurring. Similarly, converting hexadecimal based numbers back into binary is simply the reverse operation.
Then the main characteristics of a Hexadecimal Numbering System is that there are 16 distinct counting digits from 0 to F with each digit having a weight or value of 16 starting from the least significant bit (LSB). In order to distinguish Hexadecimal numbers from Denary numbers, a prefix of either a “#”, (Hash) or a “$” (Dollar sign) is used before the actual Hexadecimal Number value, #D5CF or $D5CF.
As the base of a hexadecimal system is 16, which also represents the number of individual symbols used in the system, the subscript 16 is used to identify a number expressed in hexadecimal. For example, the previous hexadecimal number is expressed as: D5CF16
Counting using Hexadecimal Numbers
So we now know how to convert 4 binary digits into a hexadecimal number. But what if we had more than 4 binary digits how would we count in hexadecimal beyond the final letter F. The simple answer is to start over again with another set of 4 bits as follows.
0…to…9, A,B,C,D,E,F, 10…to…19, 1A, 1B, 1C, 1D, 1E, 1F, 20, 21….etc
Do not get confused, 10 or 20 is NOT ten or twenty it is 1 + 0 and 2 + 0 in hexadecimal. In fact twenty does not even exist in hex. With two hexadecimal numbers we can count up to FF which is equal to decimal 255. Likewise, to count higher than FF we would add a third hexadecimal digit to the left so the first 3-bit hexadecimal number would be 10016,(25610) and the last would be FFF16, (409510). The maximum 4-digit hexadecimal number is FFFF16 which is equal to 65,535 in decimal and so on.
Representation of a Hexadecimal Number
| MSB | Hexadecimal Number | LSB | ||||||
| 168 | 167 | 166 | 165 | 164 | 163 | 162 | 161 | 160 |
| 4.3G | 2.6G | 16M | 1M | 65k | 4k | 256 | 16 | 1 |
This adding of additional hexadecimal digits to convert both decimal and binary numbers into an Hexadecimal Number is very easy if there are 4, 8, 12 or 16 binary digits to convert. But we can also add zero’s to the left of the most significant bit, the MSB if the number of binary bits is not a multiple of four.
For example, 110010110110012 is a fourteen bit binary number that is to large for just three hexadecimal digits only, yet too small for a four hexadecimal number. The answer is to ADD additional zero’s to the left most bit until we have a complete set of four bit binary number or multiples thereof.
Adding of Additional 0’s to a Binary Number
| Binary Number | 0011 | 0010 | 1101 | 1001 |
| Hexadecimal Number | 3 | 2 | D | 9 |
The main advantage of a Hexadecimal Number is that it is very compact and by using a base of 16 means that the number of digits used to represent a given number is usually less than in binary or decimal. Also, it is quick and easy to convert between hexadecimal numbers and binary.
Hexadecimal Numbers Example No1
Convert the following Binary number 1110 10102 into its Hexadecimal number equivalent.
| Binary Number = 111010102 | |||
| Group the bits into four’s starting from the right hand side | |||
| = | 1110 | 1010 | |
| Find the Decimal equivalent of each individual group | |||
| = | 14 | 10 | (in decimal) |
| Convert to Hexadecimal using the table above | |||
| = | E | A | (in Hex) |
| Then, the hexadecimal equivalent of the binary number1110 10102 is #EA16 |
Hexadecimal Numbers Example No2
Convert the following Hexadecimal number #3FA716 into its Binary equivalent, and also into its Decimal or Denary equivalent using subscripts to identify each numbering system.
| #3FA716 |
| = 0011 1111 1010 01112 |
| = (8192 + 4096 + 2048 + 1024 + 512 + 256 + 128 + 32 + 4 + 2 + 1) |
| = 16,29510 |
Then, the Decimal number of 16,295 can be represented as:-
#3FA716 in Hexadecimal
or
0011 1111 1010 01112 in Binary.
Hexadecimal Numbers Summary
Then to summarise. The Hexadecimal, or Hex, numbering system is commonly used in computer and digital systems to reduce large strings of binary numbers into a sets of four digits for us to easily understand. The word “Hexadecimal” means sixteen because this type of digital numbering system uses 16 different digits from 0-to-9, and A-to-F.
To convert binary numbers into hexadecimal numbers we must first divide the binary number up into a 4-bit binary word which can have any value from 010 ( 00002 ) to 1510 ( 11112 ) representing the hexadecimal equivalent of 0 through to F.
In the next tutorial about Binary Logic we will look at converting strings of binary numbers into another digital numbering system called Octal Numbers and vice versa.
Number Conversion
- Octal to Binary Conversion

The conversion is done by converting an individual octal digit to binary. Every digit must be converted to a 3-bit binary number and the resultant will be the binary equivalent of an octal number.
Example
Converting (145.56)8 to binary-

This table should be used in order to convert any octal number to binary. From the table, writing binary equivalent of each of the digit we get-
which is the binary equivalent of the octal number.
- Binary to Octal Conversion
The same table can be used in order to convert a binary number to octal. First, group the binary number into the group of three bits and write the octal equivalent of it.
Example
Octal equivalent of (11001111)2 is
The groups we got here are-
011,001,111. A zero before the number is added in order to complete the grouping in the form of three binary digits.
Now the octal equivalent of the numbers are-
3, 1, 7. So the octal number we got is (317)8.
- Octal to Decimal Conversion

The method of converting an octal number into its decimal equivalent is very simple. Just expand the number in the base of eight with its positional weight and the resultant will be a decimal number.
Example
Converting (317)8 to its decimal equivalent.
This can be done as follows-
- Decimal to Octal Conversion


This can be done by dividing the number by 8 using repeated division method known as double dabble method. The repeated division is done and the remainder is taken. It can be done as follows-
Example
Find the octal equivalent of 158.
The equivalent number in octal system is (236)8.
When there is a number in fraction or after the decimal point, that can be converted as-
Say we have to convert 0.40 to octal.
So we see that the number is repeated. This will go on and it will be a never ending process so we can approximate the result as-
(.3146…)8.